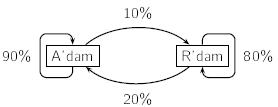
Autoverhuurbedrijf Autogo heeft twee vestigingsplaatsen: Amsterdam en Rotterdam. Klanten die in een vestigingsplaats een auto huren kunnen die in beide plaatsen terugbrengen. Dagelijks wordt er, van de auto's uit Amsterdam 10% teruggebracht in Rotterdam. De rest van de auto's wordt teruggebracht in of blijft in Amsterdam. Van de Rotterdamse auto's wordt 20% in Amsterdam ingeleverd. De rest wordt teruggebracht in of blijft in Rotterdam. Zie de onderstaande figuur voor de dagelijkse overgangspercentages. Aanvankelijk staan op beide vestigingsplaatsen evenveel auto's.
We gebruiken matrices om hierbij een dynamisch proces op te stellen.
$$\begin{equation}
\begin{pmatrix}
x_{t+1,A}\\
x_{t+1,R}\\
\end{pmatrix} =
Q
\!\!
\begin{pmatrix}
x_{t,A}\\
x_{t,R}\\
\end{pmatrix}=
\begin{pmatrix}
0.90 & 0.20\\
0.10 & 0.80\\
\end{pmatrix}\!\!\!
\begin{pmatrix}
x_{t,A}\\
x_{t,R}\\
\end{pmatrix}
\end{equation}$$
Met $x_{0,A}=x_{0,R}=\frac{1}{2}$. Hierbij is $x_{t,A}$ ($x_{t,R}$) het percentage auto's in Amsterdam (Rotterdam) op tijdstip $t$.
We gebruiken matrices om hierbij een dynamisch proces op te stellen.
$$\begin{equation}
\begin{pmatrix}
x_{t+1,A}\\
x_{t+1,R}\\
\end{pmatrix} =
Q
\!\!
\begin{pmatrix}
x_{t,A}\\
x_{t,R}\\
\end{pmatrix}=
\begin{pmatrix}
0.90 & 0.20\\
0.10 & 0.80\\
\end{pmatrix}\!\!\!
\begin{pmatrix}
x_{t,A}\\
x_{t,R}\\
\end{pmatrix}
\end{equation}$$
Met $x_{0,A}=x_{0,R}=\frac{1}{2}$. Hierbij is $x_{t,A}$ ($x_{t,R}$) het percentage auto's in Amsterdam (Rotterdam) op tijdstip $t$.