Introduction: Not every power function is integer.
Definition: A function of the form
\[
y(x)=x^{\frac{m}{n}},
\]
with $m$ and $n$ integer ($n \neq 0$), is called a power function.
Remark: If $\frac{m}{n}$ is not integer, then the domain is restricted to $x\geq 0$.
Example: $y(x)=x^{-\frac{5}{6}}=\dfrac{1}{\sqrt[6]{x^5}}$ is an example of a power function.
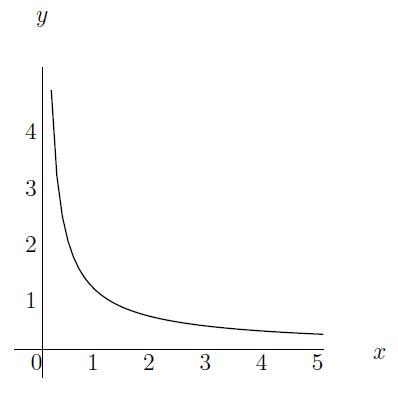
Definition: A function of the form
\[
y(x)=x^{\frac{m}{n}},
\]
with $m$ and $n$ integer ($n \neq 0$), is called a power function.
Remark: If $\frac{m}{n}$ is not integer, then the domain is restricted to $x\geq 0$.
Example: $y(x)=x^{-\frac{5}{6}}=\dfrac{1}{\sqrt[6]{x^5}}$ is an example of a power function.