Introduction: Not every power function is integer.
Definition: A function of the form
y(x)=xmn,
with m and n integer (n≠0), is called a power function.
Remark: If mn is not integer, then the domain is restricted to x≥0.
Example: y(x)=x−56=16√x5 is an example of a power function.
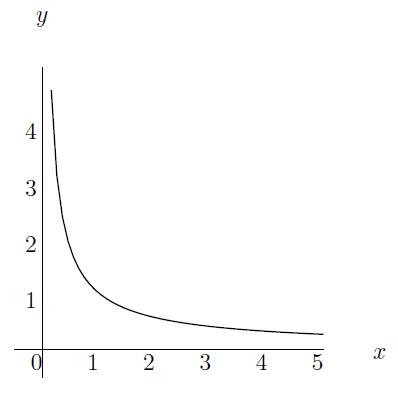
Definition: A function of the form
y(x)=xmn,
with m and n integer (n≠0), is called a power function.
Remark: If mn is not integer, then the domain is restricted to x≥0.
Example: y(x)=x−56=16√x5 is an example of a power function.


