Definition: A function of the form
z(x,y)=ax+by+c,
where a,b and c are numbers such that not both a and b equal zero, is called a linear function of two variables.
Remark 1: For a=b=0 this is a constant function of two variables.
The graph of a linear function is a plane.
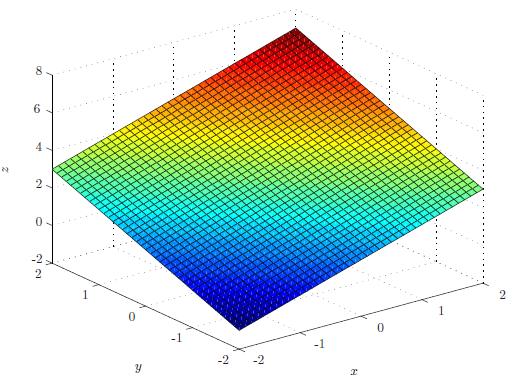
Example: The function z(x,y)=3+x+y is an example of a linear function.
z(x,y)=ax+by+c,
where a,b and c are numbers such that not both a and b equal zero, is called a linear function of two variables.
Remark 1: For a=b=0 this is a constant function of two variables.
Example: The function z(x,y)=3+x+y is an example of a linear function.


