Definition: A function of the form
z(x,y)=kxαy1−α,(x>0,y>0)
where k>0, 0≤α≤1, is called a Cobb-Douglas function.
Remark 1: Sometimes, also functions of the form z(x,y)=kxαyβ, with k>0, α>0 and β>0 are called Cobb-Douglas functions. Given this definition also z(x,y)=4x2y4 is a Cobb-Douglas function for example.
Remark 2: Cobb-Douglas functions often appear in microeconomics dues to desirable properties.
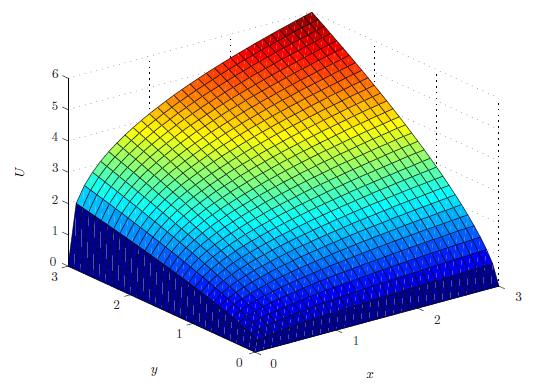
Example: An example of a Cobb-Douglas function is U(x,y)=2x13y23.
z(x,y)=kxαy1−α,(x>0,y>0)
where k>0, 0≤α≤1, is called a Cobb-Douglas function.
Remark 1: Sometimes, also functions of the form z(x,y)=kxαyβ, with k>0, α>0 and β>0 are called Cobb-Douglas functions. Given this definition also z(x,y)=4x2y4 is a Cobb-Douglas function for example.
Remark 2: Cobb-Douglas functions often appear in microeconomics dues to desirable properties.
Example: An example of a Cobb-Douglas function is U(x,y)=2x13y23.


