Definition: A function of the form
y(x)=ax+b,
where a and b are numbers (a≠0), is called a linear function.
Remark 1: For a=0 this is a constant function.
Remark 2: The graph of a linear function is a straight line.
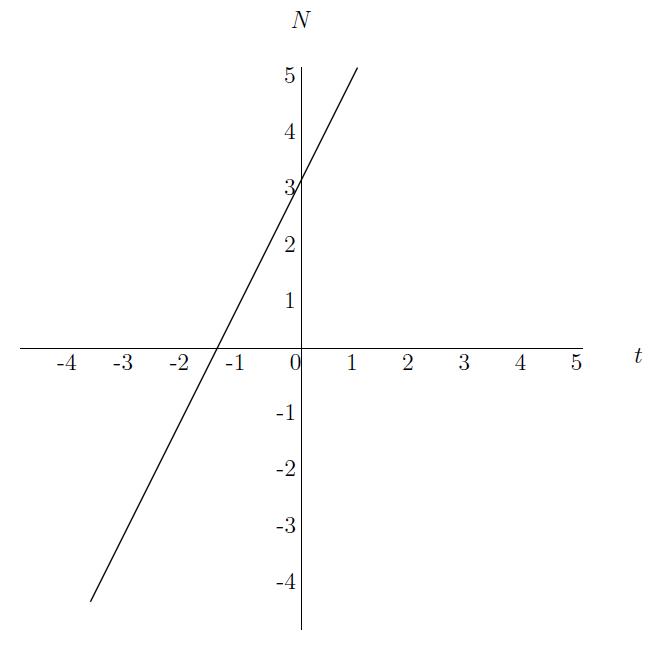
Example: De function N(t)=2t+3 is an example of a linear function.
y(x)=ax+b,
where a and b are numbers (a≠0), is called a linear function.
Remark 1: For a=0 this is a constant function.
Remark 2: The graph of a linear function is a straight line.
Example: De function N(t)=2t+3 is an example of a linear function.


