Definition: A function of the form
y(x)=alogx,
where a (a≠1) is a positive number is called a logarithmic function with base a.
Remark: The function y(x)=alogx is not defined for a=1.
Extra explanation: Every logarithmic function y(x) has one zero: x=1.
Example: y(x)=2logx is an example of a logarithmic function.
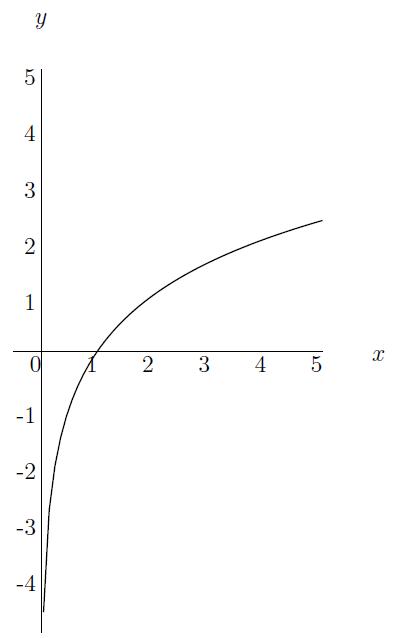
y(x)=alogx,
where a (a≠1) is a positive number is called a logarithmic function with base a.
Remark: The function y(x)=alogx is not defined for a=1.
Extra explanation: Every logarithmic function y(x) has one zero: x=1.
Example: y(x)=2logx is an example of a logarithmic function.


