Introduction: A function of the form y(x)=xk, with k a non-negative integer is called a Positive integer power function.
Definition: A function of the form
x−k=1xk,
with k a positive integer, is a negative integer power function.
Example: f(x)=x−5=1x5 is an example of a negative integer power function.
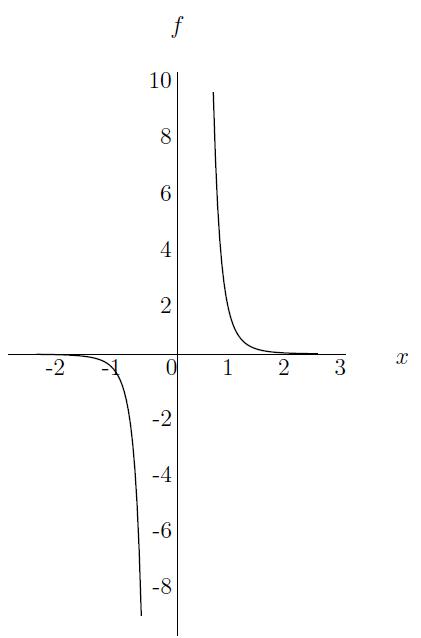
Definition: A function of the form
x−k=1xk,
with k a positive integer, is a negative integer power function.
Example: f(x)=x−5=1x5 is an example of a negative integer power function.


