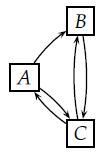
Beschouw het onderstaande netwerk met drie pagina's.
Bepaal welke webpagina het belangrijkst is.
pagina A
pagina B
pagina B en C
pagina C
Correct: De overgangsmatrix ziet er als volgt uit:
G=(0012120121210)
De uitgebreide matrix van G−I geeft het volgende.
(−1012|012−112|0121−1|0)
Vegen geeft onderstaande matix.
(10−12|00134|0000|0)
Dit geeft x1=12x3, x2=34x3 en samen met x1+x2+x3=1 geeft dit het volgende evenwicht.
(291349)
Dus C is de belangrijkste pagina.
Ga door.
Fout: Pagina A krijgt maar één verwijzing.
Zie Voorbeeld.
Fout: Pagina B is niet het belangrijkst.
Zie Voorbeeld.
Fout: B en C zijn niet even belangrijk.
Zie Voorbeeld.