Voorbeeld

In een netwerk van drie pagina's verwijst $A$ naar $B$, $B$ naar $C$ en $C$ naar zowel $A$ als $B$: zie het onderstaande plaatje.


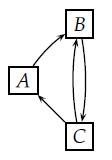
We gebruiken het idee achter het Stappenplan om tot een ranking te komen van deze pagina's. De overgangsmatrix wordt gegeven door onderstaande matrix.


$$\begin{equation}
G=\begin{pmatrix}
  0&  0 & \frac{1}{2}\\
1&  0 & \frac{1}{2}\\
0& 1 & 0\\
\end{pmatrix}
\end{equation}$$

We bepalen het evenwicht. Daarvoor bepalen we eerst $G-I_3$.

$$\begin{equation}
G-I_3=\begin{pmatrix}
  -1&  0 & \frac{1}{2}\\
1&  -1 & \frac{1}{2}\\
0& 1 & -1\\
\end{pmatrix}
\end{equation}$$

We stellen $(G-I_3)\underline{x}$ gelijk aan $\underline{0}$ en we krijgen de uitgebreide matrix.

$$\begin{equation}
\begin{pmatrix}
  -1&  0 & \frac{1}{2}&|& 0\\
1&  -1 & \frac{1}{2}&|& 0\\
0& 1 & -1 & | & 0\\
\end{pmatrix}
\end{equation}$$

Dit vegen we naar onderstaande matrix.

$$\begin{equation}
\begin{pmatrix}
1 & 0 & -\frac{1}{2} &|& 0\\
0 & 1& -1&|& 0\\
0 & 0 & 0 &| & 0\\
\end{pmatrix}
\end{equation}$$

Dus $x_1=\frac{1}{2}x_3$ en $x_2=x_3$. Verder geldt $x_1+x_2+x_3=1$, omdat $\underline{x}$ een toestandsvector is. Dit levert onderstaand evenwicht op.

$$\begin{equation}
\begin{pmatrix}
\frac{1}{5}\\
\frac{2}{5}\\
\frac{2}{5}\\
\end{pmatrix}
\end{equation}$$

Dus pagina $B$ en $C$ eindigen gelijk, pagina $A$ is laatste.