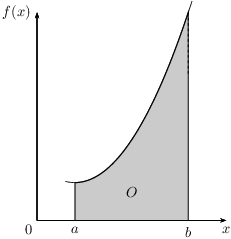
From the theorem on integrals and areas it follows that there is a relation between the integral and the area of a region below/above the graph of a function. We discuss this relation in more detail. Consider the area O(f,a,b) of the region enclosed by the graph of the function f(x), the x-axis and the lines x=a and x=b, shown in the following figure.
In general it is not easy to calculate the area when f(x) is non-linear. We can provide an approximation for the area by splitting the interval [a,b] up into smaller subintervals. For each subinterval we determine the area of the bar that best fits below the graph of f(x). When we sum the areas of these bars we obtain a reasonable lower-bound for the area of O(f,a,b). In the following figure we use for instance three bars to approximate the area O(f,a,b), hence, O(f,a,b)≈O1+O2+O3.

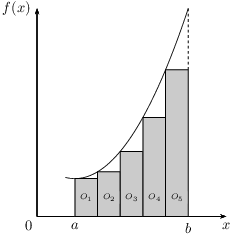
By increasing the number of subintervals we improve the approximation. In the following figure we use five bars to approximate the area of O(f,a,b), hence O(f,a,b)≈O1+O2+O3+O4+O5.
If the number of bars becomes infinite, then the approximation becomes exact and we can replace the ≈-sign by a =-sign. Hence, O(f,a,b)=O1+O2+…+On, with n an infinitely large number.

In general it is not easy to calculate the area when f(x) is non-linear. We can provide an approximation for the area by splitting the interval [a,b] up into smaller subintervals. For each subinterval we determine the area of the bar that best fits below the graph of f(x). When we sum the areas of these bars we obtain a reasonable lower-bound for the area of O(f,a,b). In the following figure we use for instance three bars to approximate the area O(f,a,b), hence, O(f,a,b)≈O1+O2+O3.

By increasing the number of subintervals we improve the approximation. In the following figure we use five bars to approximate the area of O(f,a,b), hence O(f,a,b)≈O1+O2+O3+O4+O5.

If the number of bars becomes infinite, then the approximation becomes exact and we can replace the ≈-sign by a =-sign. Hence, O(f,a,b)=O1+O2+…+On, with n an infinitely large number.

