Beschouw een code met codewoorden c1,…,cn. Door de afstand tussen ieder tweetal codewoorden (ci,cj) te bepalen, kunnen we ook de minimale afstand dmin bepalen. Wat vertelt de waarde van deze dmin ons nu precies?
Voorbeeld 1 Stel dat we voor bovengenoemde code dmin=2 vinden. Dit wil zeggen dat ieder tweetal codewoorden (ci,cj) op minstens 2 posities van elkaar verschilt. Waar bij ci op een bepaalde positie bijvoorbeeld een 1 staat, staat bij cj een 0 (of andersom). Wanneer we codewoord ci versturen en ci ontvangen zijn er blijkbaar geen fouten opgetreden. Ontvangen we echter een woord dat op precies één positie verschilt van ci, dan hebben we een probleem. Het kan zo zijn dat codewoord ci verstuurd is en er precies één fout is opgetreden. Het is echter ook mogelijk dat codewoord cj verstuurd is en er (wederom) precies één fout is opgetreden. Dit wordt geïllustreerd in de eerste regel van onderstaand plaatje. We kunnen deze ene fout dus wel herkennen maar niet herstellen. We noemen de code daarom 1-foutherkennend en 0-foutherstellend.
Voorbeeld 2 Stel nu dat we voor bovengenoemde code dmin=5 vinden. Ieder tweetal codewoorden verschilt nu op minstens 5 posities van elkaar. Wanneer er 1, 2, 3 of 4 fouten optreden, dan herkennen we dit direct. Het rijtje bits dat we ontvangen bij dit aantal fouten zal nooit een codewoord kunnen zijn, omdat er op minstens 5 posities fouten moeten optreden om een ander codewoord te vormen (zie de laatste regel van onderstaand plaatje). Welke fouten kunnen we herstellen? Dat is het aantal fouten dat dichter bij ci ligt dan bij cj, in dit geval dus maximaal 2. We noemen de code daarom 4-foutherkennend en 2-foutherstellend.
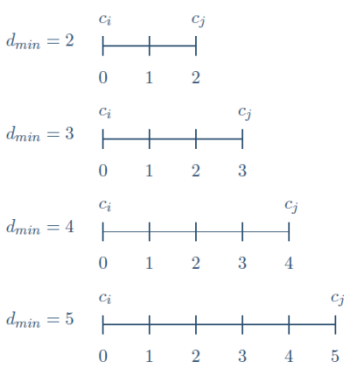
Probeer ook eens voor dmin=3 en dmin=4 het foutherkennend en foutherstellend vermogen te bepalen.
Voorbeeld 1 Stel dat we voor bovengenoemde code dmin=2 vinden. Dit wil zeggen dat ieder tweetal codewoorden (ci,cj) op minstens 2 posities van elkaar verschilt. Waar bij ci op een bepaalde positie bijvoorbeeld een 1 staat, staat bij cj een 0 (of andersom). Wanneer we codewoord ci versturen en ci ontvangen zijn er blijkbaar geen fouten opgetreden. Ontvangen we echter een woord dat op precies één positie verschilt van ci, dan hebben we een probleem. Het kan zo zijn dat codewoord ci verstuurd is en er precies één fout is opgetreden. Het is echter ook mogelijk dat codewoord cj verstuurd is en er (wederom) precies één fout is opgetreden. Dit wordt geïllustreerd in de eerste regel van onderstaand plaatje. We kunnen deze ene fout dus wel herkennen maar niet herstellen. We noemen de code daarom 1-foutherkennend en 0-foutherstellend.
Voorbeeld 2 Stel nu dat we voor bovengenoemde code dmin=5 vinden. Ieder tweetal codewoorden verschilt nu op minstens 5 posities van elkaar. Wanneer er 1, 2, 3 of 4 fouten optreden, dan herkennen we dit direct. Het rijtje bits dat we ontvangen bij dit aantal fouten zal nooit een codewoord kunnen zijn, omdat er op minstens 5 posities fouten moeten optreden om een ander codewoord te vormen (zie de laatste regel van onderstaand plaatje). Welke fouten kunnen we herstellen? Dat is het aantal fouten dat dichter bij ci ligt dan bij cj, in dit geval dus maximaal 2. We noemen de code daarom 4-foutherkennend en 2-foutherstellend.

Probeer ook eens voor dmin=3 en dmin=4 het foutherkennend en foutherstellend vermogen te bepalen.

