Beschouw de onderstaande onderhoudssituatie.
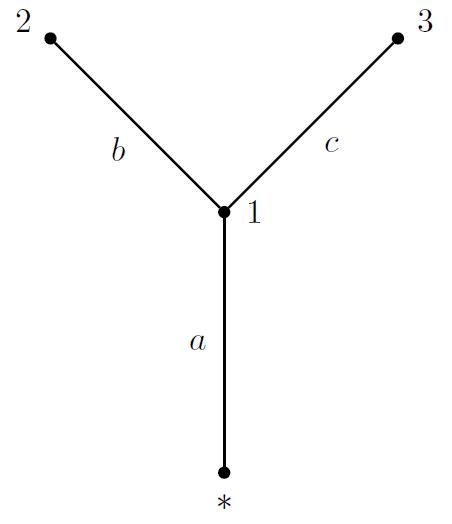
Een extreem punt van de core van het bijbehorende onderhoudsspel is $(4,1,3)$. Wat zijn $a$, $b$ en $c$?
Dat is niet te bepalen met deze informatie.
$a=8$, $b=0$, en $c=0$.
$a=1\frac{1}{3}$, $b=2\frac{1}{3}$ en $c=4\frac{1}{3}$.
$a=4$, $b=1$ en $c=3$.
Correct: Omdat het een onderhoudsspel is geldt dat een extreem punt van de core een marginale vector is. Deze kun je vinden door voor iedere volgorde van de spelers een speler die kosten toe te kennen die hij maakt om alle verbinding tussen hemzelf en de bron, die nog niet door een voorganger zijn onderhouden, te onderhouden; zie de tabel hieronder.
| $\sigma$ | $m^{\sigma}$ |
| $(1,2,3)$ | $(a, b, c)$ |
| $(1,3,2)$ | $(a, b, c)$ |
| $(2,1,3)$ | $(0, a+b, c)$ |
| $(2,3,1)$ | $(0, a+b, c)$ |
| $(3,2,1)$ | $(0, b, a+c)$ |
| $(3,1,2)$ | $(0, b, a+c)$ |
Dit betekent dat in een marginale vector speler 1 of $a$ of $0$ betaalt, dus $a=4$. In een marginale vector waarin speler 1 een bijdrage heeft van $a$ hebben spelers 2 en 3 een bijdrage van $b$ en $c$ respectievelijk, dus $b=1$ en $c=4$.
Fout: Omdat het een onderhoudsspel is geldt dat een extreem punt van de core een marginale vector is. Deze kun je vinden door voor iedere volgorde van de spelers een speler die kosten toe te kennen die hij maakt om alle verbinding tussen hemzelf en de bron, die nog niet door een voorganger zijn onderhouden, te onderhouden.
Probeer de opgave nogmaals.
Fout: Omdat het een onderhoudsspel is geldt dat een extreem punt van de core een marginale vector is. Deze kun je vinden door voor iedere volgorde van de spelers een speler die kosten toe te kennen die hij maakt om alle verbinding tussen hemzelf en de bron, die nog niet door een voorganger zijn onderhouden, te onderhouden.
Probeer de opgave nogmaals.
Fout: Omdat het een onderhoudsspel is geldt dat een extreem punt van de core een marginale vector is. Deze kun je vinden door voor iedere volgorde van de spelers een speler die kosten toe te kennen die hij maakt om alle verbinding tussen hemzelf en de bron, die nog niet door een voorganger zijn onderhouden, te onderhouden.
Probeer de opgave nogmaals.