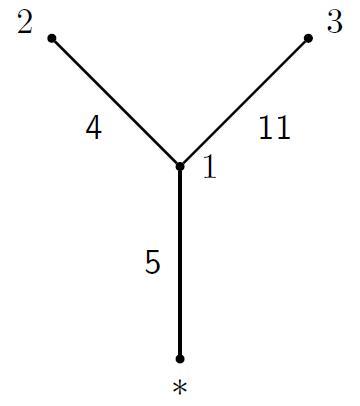
We beschouwen de onderstaande onderhoudssituatie.
Het spel $(N,c)$ staat in de onderstaande tabel. (Zie Shapleywaarde en onderhoudsregel: Voorbeeld.)
| $S$ | $\{1\}$ | $\{2\}$ | $\{3\}$ | $\{1,2\}$ | $\{1,3\}$ | $\{2,3\}$ | $N$ |
| $c(S)$ | $5$ | $9$ | $16$ | $9$ | $16$ | $20$ | $20$ |
De marginale vectoren van het spel $(N,c)$ worden gegeven in de onderstaande tabel. (Zie Shapleywaarde en onderhoudsregel: Voorbeeld.)
| $\sigma$ | $m^{\sigma}$ |
| $(1,2,3)$ | $(5,4,11)$ |
| $(1,3,2)$ | $(5,4,11)$ |
| $(2,1,3)$ | $(0,9,11)$ |
| $(2,3,1)$ | $(0,9,11)$ |
| $(3,2,1)$ | $(0,4,16)$ |
| $(3,1,2)$ | $(0,4,16)$ |
De core van het bovenstaande spel wordt gegeven in het onderstaande plaatje. (Zie Core kostenspel: Voorbeeld (film).)
Je ziet dat de marginale vectoren exact overeenkomen met de extreme punten van de core; $(0,4,16)$, $(0,9,11)$, $(5,4,11)$. Dit betekent onder andere dat de Shapleywaarde, $\varphi(v)=(1\frac{2}{3},5\frac{2}{3},12\frac{2}{3})$, in de core van het kostenspel ligt.