Definitie: Een functie van de vorm
z(x,y)=kxαy1−α,
waarbij k>0, 0≤α≤1, wordt een Cobb-Douglas functie genoemd.
Opmerking 1: Het domein van deze functie bestaat uit alle combinaties van positieve waarden van x en y, oftewel, x>0 en y>0.
Opmerking 2: In de literatuur worden soms ook functies van de vorm z(x,y)=xαyβ, waarbij k>0, α>0 and β>0, Cobb-Douglas functies genoemd. In deze definitie is z(x,y)=4x2y4 dus ook een Cobb-Douglas functie.
Opmerking 3: Cobb-Douglas functies komen in de micro-economie nogal eens voor vanwege de handige eigenschappen.
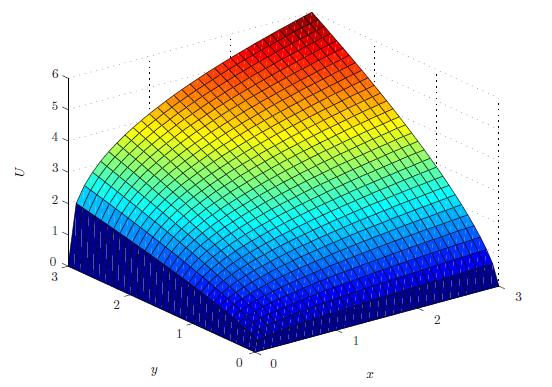
Voobeeld: Een voorbeeld van een Cobb-Douglas functie is U(x,y)=2x13y23.
z(x,y)=kxαy1−α,
waarbij k>0, 0≤α≤1, wordt een Cobb-Douglas functie genoemd.
Opmerking 1: Het domein van deze functie bestaat uit alle combinaties van positieve waarden van x en y, oftewel, x>0 en y>0.
Opmerking 2: In de literatuur worden soms ook functies van de vorm z(x,y)=xαyβ, waarbij k>0, α>0 and β>0, Cobb-Douglas functies genoemd. In deze definitie is z(x,y)=4x2y4 dus ook een Cobb-Douglas functie.
Opmerking 3: Cobb-Douglas functies komen in de micro-economie nogal eens voor vanwege de handige eigenschappen.
Voobeeld: Een voorbeeld van een Cobb-Douglas functie is U(x,y)=2x13y23.


