Definitie: Een functie van de vorm
z(x,y)=min{ax,by},
waarbij a>0 en b>0 wordt een minimumfunctie genoemd.
Opmerking: De functiewaarde wordt bepaald door het element (ax of by) dat de laagste waarde heeft. We kunnen de functie daarom ook opschrijven als
z(x,y)={axals~ax≤by,byals~ax>by.
Voorbeeld: De functie z(x,y)=min{3x,4y} is een voorbeeld van een minimumfunctie.
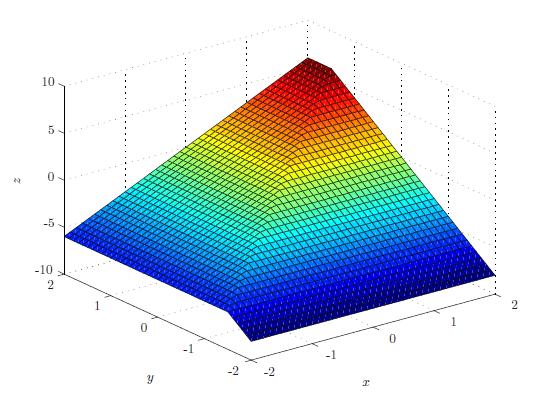
z(x,y)=min{ax,by},
waarbij a>0 en b>0 wordt een minimumfunctie genoemd.
Opmerking: De functiewaarde wordt bepaald door het element (ax of by) dat de laagste waarde heeft. We kunnen de functie daarom ook opschrijven als
z(x,y)={axals~ax≤by,byals~ax>by.
Voorbeeld: De functie z(x,y)=min{3x,4y} is een voorbeeld van een minimumfunctie.


