Introductie: Een functie van de vorm $y(x)=x^k$, met $k$ een niet-negatief geheel getal wordt een Positief geheeltallige machtsfunctie genoemd.
Definitie: Een functie van de vorm
\[
x^{-k}=\frac{1}{x^k},
\]
met $k$ een niet-negatief geheel getal, is een negatief geheeltallige machtfunctie.
Voorbeeld: $f(x)=x^{-5}=\dfrac{1}{x^5}$ is een voorbeeld van een negatief geheeltallige machtfunctie.
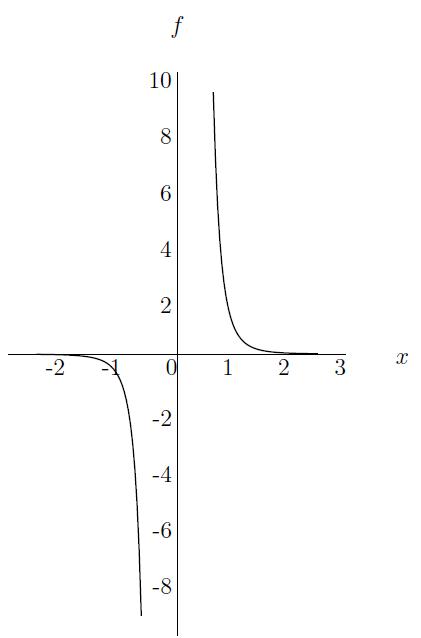
Definitie: Een functie van de vorm
\[
x^{-k}=\frac{1}{x^k},
\]
met $k$ een niet-negatief geheel getal, is een negatief geheeltallige machtfunctie.
Voorbeeld: $f(x)=x^{-5}=\dfrac{1}{x^5}$ is een voorbeeld van een negatief geheeltallige machtfunctie.