Introductie: Niet iedere machtsfunctie is geheeltallig.
Definitie: Een functie van de vorm
\[
y(x)=x^{\frac{m}{n}},
\]
waarbij $m$ en $n$ geheeltallig zijn ($n \neq 0$), wordt een machtsfunctie genoemd.
Opmerking: Als $\frac{m}{n}$ niet geheeltallig is dan is het domein beperkt tot $x\geq 0$.
Voorbeeld: $y(x)=x^{-\frac{5}{6}}=\dfrac{1}{\sqrt[6]{x^5}}$ is een voorbeeld van een machtsfunctie.
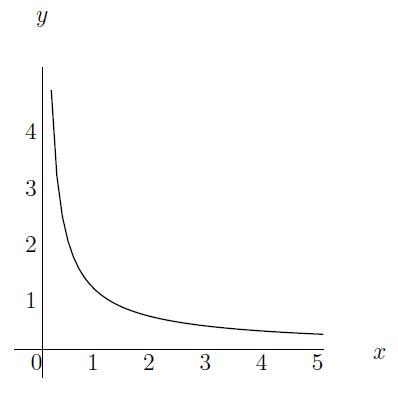
Definitie: Een functie van de vorm
\[
y(x)=x^{\frac{m}{n}},
\]
waarbij $m$ en $n$ geheeltallig zijn ($n \neq 0$), wordt een machtsfunctie genoemd.
Opmerking: Als $\frac{m}{n}$ niet geheeltallig is dan is het domein beperkt tot $x\geq 0$.
Voorbeeld: $y(x)=x^{-\frac{5}{6}}=\dfrac{1}{\sqrt[6]{x^5}}$ is een voorbeeld van een machtsfunctie.