Definitie: Voor alle x>0 geldt dat een functie van de vorm
y(x)=alogx,
waarbij a (a≠1) een postief getal is een exponentiële functie met grondtal a wordt genoemd.
Opmerking: De functie y(x)=alogx is niet gedefinieerd voor a=1.
Extra uitleg: Iedere logaritmische functie y(x) heeft één nulpunt: x=1.
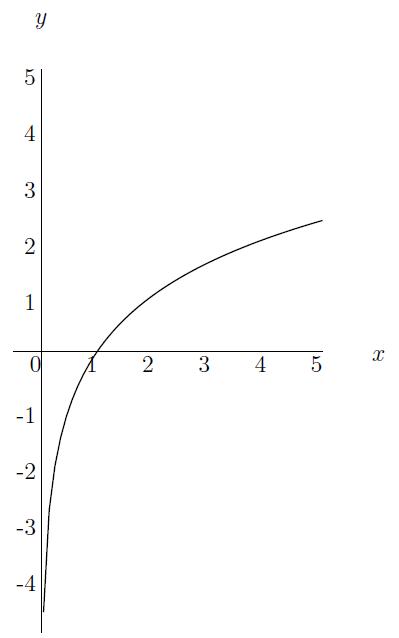
Voorbeeld: y(x)=2logx is een voorbeeld van een logaritmische functie.
y(x)=alogx,
waarbij a (a≠1) een postief getal is een exponentiële functie met grondtal a wordt genoemd.
Opmerking: De functie y(x)=alogx is niet gedefinieerd voor a=1.
Extra uitleg: Iedere logaritmische functie y(x) heeft één nulpunt: x=1.
Voorbeeld: y(x)=2logx is een voorbeeld van een logaritmische functie.


