Definitie: Een functie van de vorm
z(x,y)=ax+by+c,
waarbij a, b en c getallen zijn waarbij a en b niet beiden gelijk aan nul zijn, wordt een lineaire functie van twee variabelen genoemd.
Opmerking 1: Voor a=b=0 is dit een constante functie van twee variabelen.
Opmerking 2: De grafiek van een lineaire functie is een vlak.
Voorbeeld: De functie z(x,y)=3+x+y is een voorbeeld van een lineaire functie.
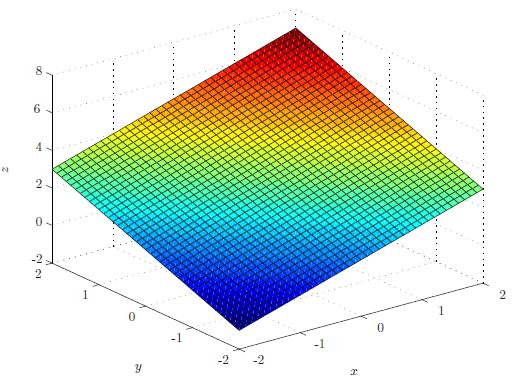
z(x,y)=ax+by+c,
waarbij a, b en c getallen zijn waarbij a en b niet beiden gelijk aan nul zijn, wordt een lineaire functie van twee variabelen genoemd.
Opmerking 1: Voor a=b=0 is dit een constante functie van twee variabelen.
Opmerking 2: De grafiek van een lineaire functie is een vlak.
Voorbeeld: De functie z(x,y)=3+x+y is een voorbeeld van een lineaire functie.


