Example 2

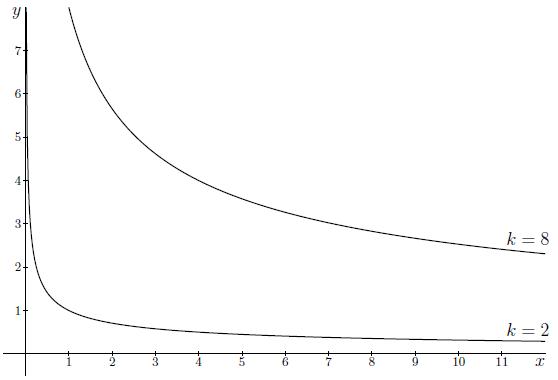
We consider the function $U(x,y) =2x^{\tfrac{1}{3}}y^{\tfrac{2}{3}}$. The graph of this function can be found here: Cobb-Douglas functions. Here we draw the indifference curves of $U(x,y)$ with values $k=2$ and $k=8$.

We start with the indifference curve for $k=2$. We determine the curve that connects all the points $(x,y)$ such that
$$\begin{align} 2x^{\tfrac{1}{3}}y^{\tfrac{2}{3}} &= 2\\ x^{\tfrac{1}{3}}y^{\tfrac{2}{3}} &= 1\\\ y^{\tfrac{2}{3}} &= x^{-\tfrac{1}{3}}\\ y &= \left(x^{-\tfrac{1}{3}}\right)^{\tfrac{3}{2}} = x^{-\tfrac{1}{2}} = \dfrac{1}{\sqrt{x}}. \end{align}$$

The second indifference curve, with value $k=8$, is determined in the same way. We determine the curve that connects all the points $(x,y)$ such that
$$\begin{align} 2x^{\tfrac{1}{3}}y^{\tfrac{2}{3}} &= 8\\ x^{\tfrac{1}{3}}y^{\tfrac{2}{3}} &= 4\\\ y^{\tfrac{2}{3}} &= 4x^{-\tfrac{1}{3}}\\ y &= \left(4x^{-\tfrac{1}{3}}\right)^{\tfrac{3}{2}}=4^{\tfrac{3}{2}}\left(x^{-\tfrac{1}{3}}\right)^{\tfrac{3}{2}} = 8x^{-\tfrac{1}{2}} = \dfrac{8}{\sqrt{x}}. \end{align}$$

In the coordinate system below both indifference curves are shown.