We consider the function $z(x,y) = \min\{3x,4y\}$. The graph of this function can be found here: Minimum functions. In this example we draw the level curve of $z(x,y)$ with value $k=6$.
The level curve is given by
$$ z(x,y) = \min\{3x,4y\} = 6.$$
Using the alternative notation (see Minimum functions), then we can write this equation as
$$ \left\{ \begin{array}{ll}
3x = 6& \text{if~}4y\geq 6,\\
4y = 6 & \text{if~}3x \geq 6.
\end{array} \right.$$
We can simplify it to
$$ \left\{ \begin{array}{ll}
x = 2 & \text{if~}y\geq \tfrac{3}{2},\\
y = \tfrac{3}{2} & \text{if~}x \geq 2.
\end{array} \right.$$
We draw the two lines, $x=2$ and $y=\tfrac{3}{2}$, in a $(x,y)$-coordinate system. These are the dashed lines in the left figure.
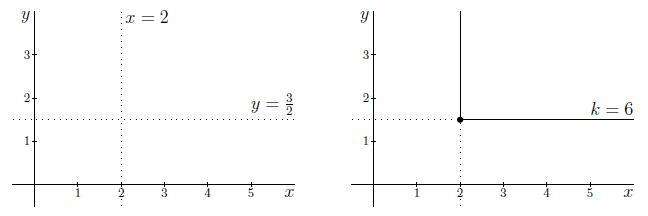
Then we use the 'if'-restrictions.
If $y\geq\tfrac{3}{2}$, then the level curve is given by $x=2$. This is the vertical part of the line in the right figure.
If $x\geq 2$, then the level curve is given by $y=\tfrac{3}{2}$; this is the horizontal part of the line in the right figure. These lines together form the level curve of $z(x,y)$ with value $k=6$.
