Which of the following graphs depicts the indifference curves of the utility function $U(x,y)=4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}$, $(x>0, y>0)$ with values $k=2$, $k=4$ and $k=8$?
Antwoord 1 correct
Correct
Antwoord 2 optie
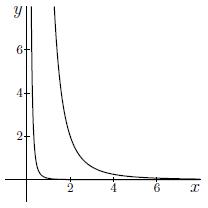
Antwoord 2 correct
Fout
Antwoord 3 optie
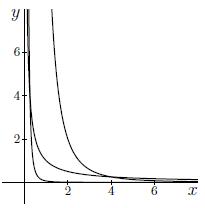
Antwoord 3 correct
Fout
Antwoord 4 optie
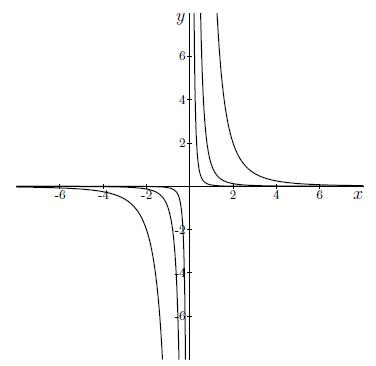
Antwoord 4 correct
Fout
Antwoord 1 optie
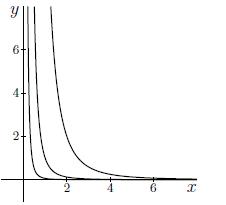
Antwoord 1 feedback
Correct: We are dealing with a utility function that is only defined for $x>0$ and $y>0$. The rewriting of $4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}} = k$ for $k=2$ gives:
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 2 \iff y^{\tfrac{1}{4}} = \dfrac{1}{2x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{1}{16x^3} \stackrel{y\geq0}{=}\dfrac{1}{16x^3}.$$
The graph of this is the left curve. The rewriting of $4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}} = k$ for $k=4$ gives:
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 4 \iff y^{\tfrac{1}{4}} = \dfrac{1}{x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{1}{x^3} \stackrel{y\geq0}{=}\dfrac{1}{x^3}.$$
The graph of this is the curve in the middle. The rewriting of $4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}} = k$ for $k=8$ gives:
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 8 \iff y^{\tfrac{1}{4}} = \dfrac{2}{x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{16}{x^3} \stackrel{x\geq0}{=}\dfrac{16}{x^3}.$$
The graph of this is the curve is the right curve.
Go on.
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 2 \iff y^{\tfrac{1}{4}} = \dfrac{1}{2x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{1}{16x^3} \stackrel{y\geq0}{=}\dfrac{1}{16x^3}.$$
The graph of this is the left curve. The rewriting of $4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}} = k$ for $k=4$ gives:
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 4 \iff y^{\tfrac{1}{4}} = \dfrac{1}{x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{1}{x^3} \stackrel{y\geq0}{=}\dfrac{1}{x^3}.$$
The graph of this is the curve in the middle. The rewriting of $4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}} = k$ for $k=8$ gives:
$$4x^{\tfrac{3}{4}}y^{\tfrac{1}{4}}= 8 \iff y^{\tfrac{1}{4}} = \dfrac{2}{x^{\tfrac{3}{4}}} \iff y = \pm\dfrac{16}{x^3} \stackrel{x\geq0}{=}\dfrac{16}{x^3}.$$
The graph of this is the curve is the right curve.
Go on.
Antwoord 2 feedback
Wrong: How many indifference curves are asked for?
Try again.
Try again.
Antwoord 3 feedback
Wrong: Level curves, and hence also indifference curves, do not intersect.
See Level curves, Example 1 and Example 2.
See Level curves, Example 1 and Example 2.
Antwoord 4 feedback
Wrong: What are the domains of $x$ and $y$?
Try again.
Try again.