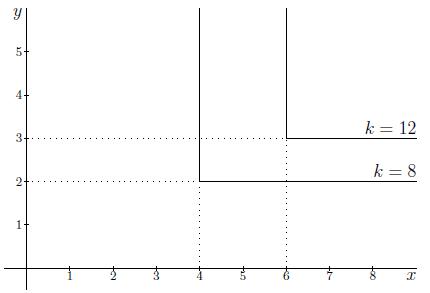
Which of the following functions corresponds to the level curve in the following graph?

Antwoord 1 correct
Correct
Antwoord 2 optie
z(x,y)=2x + 4y.
Antwoord 2 correct
Fout
Antwoord 3 optie
z(x,y)=\min\{4x,2y\}.
Antwoord 3 correct
Fout
Antwoord 4 optie
z(x,y) = \min\{x,2y\}.
Antwoord 4 correct
Fout
Antwoord 1 optie
z(x,y)=\min\{2x,4y\}.
Antwoord 1 feedback
Correct: The shape of the level curve indicates that we are dealing with a minimum function. Hence, we look for a function z(x,y) = \min\{ax,by\} of which a and b have to be determined.
You can see that ax = by at (4,2), or
a\cdot 4 = b\cdot2.
Moreover, we know that the value of z(x,y) at that point is equal to 8, hence
\min\{a\cdot 4, b\cdot 2\} = 8 \iff 4a = 8 \text{~and~} 2b = 8 \iff a = 2 \text{~and~} b=4.
Hence, the function that results in this level curve is
z(x,y) = \min\{2x,4y\}.
You can use the level curve with value k=12 to check your answer. The level curve with value 12 corresponding to the function \min\{2x,4y\} is
\left\{\begin{array}{ll} 2x = 12 & \text{if~}4y\geq12\\ 4y = 12 & \text{if~}2x\geq 12 \end{array}\right. \iff \left\{\begin{array}{ll} x = 6 & \text{if~}y\geq3\\ y = 3 & \text{if~}x\geq6 \end{array}\right.
This is exactly the level curve with value 12 as drawn in the figure.
Go on.
You can see that ax = by at (4,2), or
a\cdot 4 = b\cdot2.
Moreover, we know that the value of z(x,y) at that point is equal to 8, hence
\min\{a\cdot 4, b\cdot 2\} = 8 \iff 4a = 8 \text{~and~} 2b = 8 \iff a = 2 \text{~and~} b=4.
Hence, the function that results in this level curve is
z(x,y) = \min\{2x,4y\}.
You can use the level curve with value k=12 to check your answer. The level curve with value 12 corresponding to the function \min\{2x,4y\} is
\left\{\begin{array}{ll} 2x = 12 & \text{if~}4y\geq12\\ 4y = 12 & \text{if~}2x\geq 12 \end{array}\right. \iff \left\{\begin{array}{ll} x = 6 & \text{if~}y\geq3\\ y = 3 & \text{if~}x\geq6 \end{array}\right.
This is exactly the level curve with value 12 as drawn in the figure.
Go on.
Antwoord 2 feedback
Antwoord 3 feedback

