Which of the following functions corresponds to the level curve in the following graph?

Antwoord 1 correct
Correct
Antwoord 2 optie
z(x,y)=6x+2y.
Antwoord 2 correct
Fout
Antwoord 3 optie
y(x)=2−13x.
Antwoord 3 correct
Fout
Antwoord 4 optie
z(x,y)=min{6x,2y}.
Antwoord 4 correct
Fout
Antwoord 1 optie
z(x,y=2x+6y.
Antwoord 1 feedback
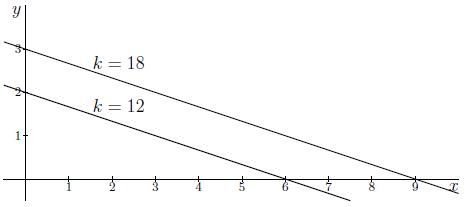
Correct: The shape of the level curves indicates that the general form of the function of which these are level curves is equal to z(x,y)=ax+by+c (see Example 1).
On the level curve with value k=12 are the points (x,y)=(0,2) and (x,y)=(6,0); hence, we know that
(1) z(0,2)=2b+c=12⟺c=12−2band(2) z(6,0)=6a+c=12⟺c=12−6a.
On the level curve with value k=18 are the points (x,y)=(0,3) and (x,y)=(9,0); hence, we know that
(3) z(0,3)=3b+c=18⟺c=18−3band(4) z(9,0)=9a+c=18⟺c=18−9a.
Combining (1) and (3) gives
12−2b=18−3bb=6c=12−2⋅6=18−3⋅6=0.
Combining (2) and (4) gives
12−6a=18−9a3a=6a=2c=12−6⋅2=18−9⋅2=0.
Hence, the function of which the level curves are given is z(x,y)=2x+6y.
Go on.
On the level curve with value k=12 are the points (x,y)=(0,2) and (x,y)=(6,0); hence, we know that
(1) z(0,2)=2b+c=12⟺c=12−2band(2) z(6,0)=6a+c=12⟺c=12−6a.
On the level curve with value k=18 are the points (x,y)=(0,3) and (x,y)=(9,0); hence, we know that
(3) z(0,3)=3b+c=18⟺c=18−3band(4) z(9,0)=9a+c=18⟺c=18−9a.
Combining (1) and (3) gives
12−2b=18−3bb=6c=12−2⋅6=18−3⋅6=0.
Combining (2) and (4) gives
12−6a=18−9a3a=6a=2c=12−6⋅2=18−9⋅2=0.
Hence, the function of which the level curves are given is z(x,y)=2x+6y.
Go on.
Antwoord 2 feedback
Antwoord 3 feedback
Wrong: This is the equation of the level curve, not of the equation of the function of which the level curve is shown..
See Example 1 and try again.
See Example 1 and try again.

