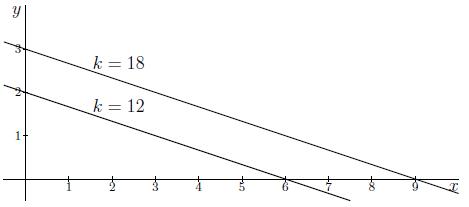
Welke van de functies past bij de niveaukromme in onderstaande grafiek?

Antwoord 1 correct
Correct
Antwoord 2 optie
z(x,y)=6x+2y.
Antwoord 2 correct
Fout
Antwoord 3 optie
y(x)=2−13x.
Antwoord 3 correct
Fout
Antwoord 4 optie
z(x,y)=min{6x,2y}.
Antwoord 4 correct
Fout
Antwoord 1 optie
z(x,y=2x+6y.
Antwoord 1 feedback
Correct: Door de vorm van de niveaukrommen weten we dat de algemene vorm van de functie waarvan dit niveaukrommen zijn, gelijk is aan z(x,y)=ax+by+c (zie Voorbeeld 1).
Op de niveaukromme met waarde k=12 liggen de punten (x,y)=(0,2) en (x,y)=(6,0); we weten dus dat
(1) z(0,2)=2b+c=12⟺c=12−2ben(2) z(6,0)=6a+c=12⟺c=12−6a.
Op de niveaukromme met waarde k=18 liggen de punten (x,y)=(0,3) en (x,y)=(9,0); we weten dus dat
(3) z(0,3)=3b+c=18⟺c=18−3ben(4) z(9,0)=9a+c=18⟺c=18−9a.
Als we (1) en (3) combineren, vinden we dat
12−2b=18−3bb=6c=12−2⋅6=18−3⋅6=0.
Als we (2) en (4) combineren, vinden we dat
12−6a=18−9a3a=6a=2c=12−6⋅2=18−9⋅2=0.
De functie waarvan de niveaukromme in bovenstaande figuur staat, is dus z(x,y)=2x+6y.
Ga door.
Op de niveaukromme met waarde k=12 liggen de punten (x,y)=(0,2) en (x,y)=(6,0); we weten dus dat
(1) z(0,2)=2b+c=12⟺c=12−2ben(2) z(6,0)=6a+c=12⟺c=12−6a.
Op de niveaukromme met waarde k=18 liggen de punten (x,y)=(0,3) en (x,y)=(9,0); we weten dus dat
(3) z(0,3)=3b+c=18⟺c=18−3ben(4) z(9,0)=9a+c=18⟺c=18−9a.
Als we (1) en (3) combineren, vinden we dat
12−2b=18−3bb=6c=12−2⋅6=18−3⋅6=0.
Als we (2) en (4) combineren, vinden we dat
12−6a=18−9a3a=6a=2c=12−6⋅2=18−9⋅2=0.
De functie waarvan de niveaukromme in bovenstaande figuur staat, is dus z(x,y)=2x+6y.
Ga door.
Antwoord 2 feedback
Fout: Waarschijnlijk maak je een foutje bij het omschrijven.
Zie Voorbeeld 1 en probeer de opgave nogmaals.
Zie Voorbeeld 1 en probeer de opgave nogmaals.
Antwoord 3 feedback
Fout: Dit is de vergelijking van de niveaukromme, niet de vergelijking van de functie waarvan dit de niveaukromme is.
Zie Voorbeeld 1 en probeer de opgave nogmaals.
Zie Voorbeeld 1 en probeer de opgave nogmaals.
Antwoord 4 feedback
Fout: Wat is de algemene vorm van de niveaukrommen van een minimumfunctie?
Zie Voorbeeld 1 en Voorbeeld 3 en probeer de opgave nogmaals.
Zie Voorbeeld 1 en Voorbeeld 3 en probeer de opgave nogmaals.

