Welke van de onderstaande grafieken geeft de niveaukrommen van $z(x,y)=x^2 + y$ met waarden $k=4$ en $k=10$ weer?
Antwoord 1 correct
Correct
Antwoord 2 optie
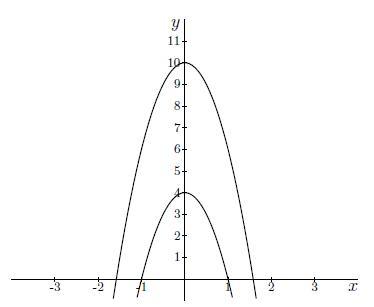
Antwoord 2 correct
Fout
Antwoord 3 optie
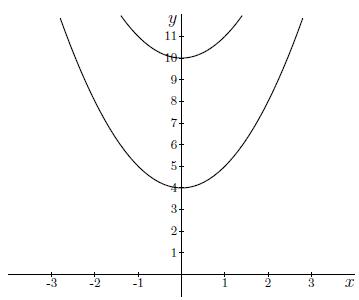
Antwoord 3 correct
Fout
Antwoord 4 optie
Antwoord 4 correct
Fout
Antwoord 1 optie
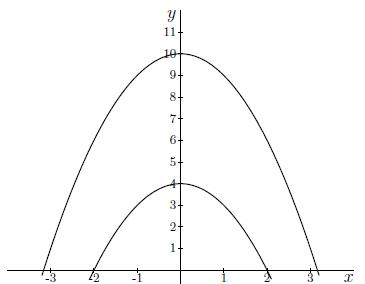
Antwoord 1 feedback
Correct: Het herschrijven van $x^2 + y = k$ voor $k=4$ geeft:
$$ x^2 + y = 4 \iff y = 4-x^2.$$
Dit is een bergparabool die de $y$-as snijdt in $(0,4)$ en de $x$-as in $(-2,0)$ en $(2,0)$ en is dus de onderste kromme van de twee. Het herschrijven van $x^2 + y = k$ voor $k=10$ geeft:
$$ x^2 + y = 10 \iff y = 10-x^2.$$
Dit is een bergparabool die de $y$-as snijdt in $(0,10)$ en de $x$-as in $(-\sqrt{10},0)$ en $(\sqrt{10},0)$ en is dus de bovenste kromme van de twee.
Ga door.
$$ x^2 + y = 4 \iff y = 4-x^2.$$
Dit is een bergparabool die de $y$-as snijdt in $(0,4)$ en de $x$-as in $(-2,0)$ en $(2,0)$ en is dus de onderste kromme van de twee. Het herschrijven van $x^2 + y = k$ voor $k=10$ geeft:
$$ x^2 + y = 10 \iff y = 10-x^2.$$
Dit is een bergparabool die de $y$-as snijdt in $(0,10)$ en de $x$-as in $(-\sqrt{10},0)$ en $(\sqrt{10},0)$ en is dus de bovenste kromme van de twee.
Ga door.
Antwoord 2 feedback
Fout: Let op het herschrijven van $z(x,y)=k$. Waarschijnlijk heb je hier een foutje gemaakt.
Zie Voorbeeld 1 en Voorbeeld 2.
Zie Voorbeeld 1 en Voorbeeld 2.
Antwoord 3 feedback
Fout: Let op het herschrijven van $z(x,y)=k$. Waarschijnlijk heb je hier een foutje gemaakt.
Zie Voorbeeld 1 en Voorbeeld 2.
Zie Voorbeeld 1 en Voorbeeld 2.
Antwoord 4 feedback
Fout: Niveaukrommen kunnen elkaar niet snijden. Waarschijnlijk heb je een foutje gemaakt in het herschrijven.
Zie Niveaukrommen, Voorbeeld 1 en Voorbeeld 2.
Zie Niveaukrommen, Voorbeeld 1 en Voorbeeld 2.