We beschouwen de functie $z(x,y) = \min\{3x,4y\}$. De grafiek van deze functie kun je hier vinden. In dit voorbeeld zullen we de niveaukromme van $z(x,y)$ tekenen voor de waarde $k=6$.
De niveaukromme wordt bepaald door
$$ z(x,y) = \min\{3x,4y\} = 6.$$
Als we de alternatieve notatie gebruiken die gegeven wordt bij de opmerking bij Minimumfuncties, dan kunnen we deze vergelijking schrijven als
$$ \left\{ \begin{array}{ll}
3x = 6& \text{als~}4y\geq 6,\\
4y = 6 & \text{als~}3x \geq 6.
\end{array} \right.$$
We kunnen dit nog vereenvoudigen naar
$$ \left\{ \begin{array}{ll}
x = 2 & \text{als~}y\geq \tfrac{3}{2},\\
y = \tfrac{3}{2} & \text{als~}x \geq 2.
\end{array} \right.$$
We tekenen de twee lijnen, $x=2$ en $y=\tfrac{3}{2}$, in een $(x,y)$-assenstelsel. Dit zijn de gestippelde lijnen in de linkerfiguur hieronder.
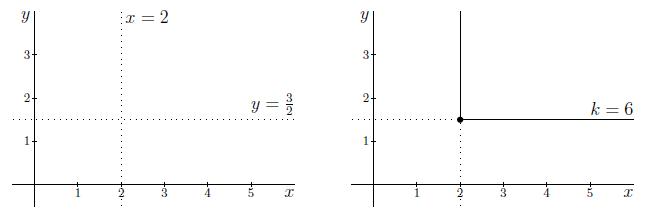
We hebben nu nog geen gebruik gemaakt van de 'als'-voorwaarden.
Als $y\geq\tfrac{3}{2}$, dan wordt de niveaukromme gegeven door $x=2$. Dit is het verticale gedeelte van de doorgetrokken lijn in de rechterfiguur.
Als $x\geq 2$, dan wordt de niveaukromme gegeven door $y=\tfrac{3}{2}$; dit is het horizontale deel van de doorgetrokken lijn in de rechterfiguur. Deze lijnen vormen samen de niveaukromme van $x(x,y)$ met waarde $k=6$.
De niveaukromme wordt bepaald door
$$ z(x,y) = \min\{3x,4y\} = 6.$$
Als we de alternatieve notatie gebruiken die gegeven wordt bij de opmerking bij Minimumfuncties, dan kunnen we deze vergelijking schrijven als
$$ \left\{ \begin{array}{ll}
3x = 6& \text{als~}4y\geq 6,\\
4y = 6 & \text{als~}3x \geq 6.
\end{array} \right.$$
We kunnen dit nog vereenvoudigen naar
$$ \left\{ \begin{array}{ll}
x = 2 & \text{als~}y\geq \tfrac{3}{2},\\
y = \tfrac{3}{2} & \text{als~}x \geq 2.
\end{array} \right.$$
We tekenen de twee lijnen, $x=2$ en $y=\tfrac{3}{2}$, in een $(x,y)$-assenstelsel. Dit zijn de gestippelde lijnen in de linkerfiguur hieronder.
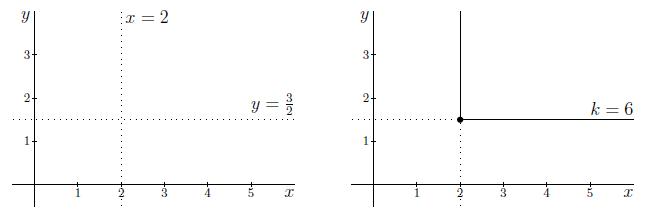
We hebben nu nog geen gebruik gemaakt van de 'als'-voorwaarden.
Als $y\geq\tfrac{3}{2}$, dan wordt de niveaukromme gegeven door $x=2$. Dit is het verticale gedeelte van de doorgetrokken lijn in de rechterfiguur.
Als $x\geq 2$, dan wordt de niveaukromme gegeven door $y=\tfrac{3}{2}$; dit is het horizontale deel van de doorgetrokken lijn in de rechterfiguur. Deze lijnen vormen samen de niveaukromme van $x(x,y)$ met waarde $k=6$.