We beschouwen de functie $z(x,y) = 3+x+y$. De grafiek van deze functie kun je vinden op Lineaire functies van twee variabelen. Hier zullen we de niveaukrommen van $z(x,y)$ tekenen met de waarden $k=5$ en $k=8$.
We beginnen met de niveaukromme voor $k=5$. Hierbij tekenen we een lijn die alle punten $(x,y)$ verbindt waarvoor geldt dat
$$\begin{align}
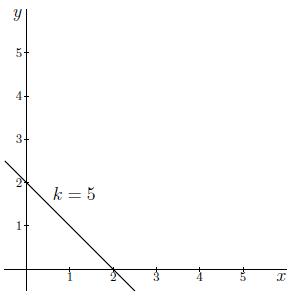
3 + x + y &= 5\\
x + y &= 2\\\
y &= 2- x.
\end{align}$$
We krijgen dus een lineaire functie die de $y$-as snijdt in $(0,2)$ en een richtingscoëfficiënt van $-1$ heeft. Als we deze lijn tekenen, krijgen we onderstaande grafiek.
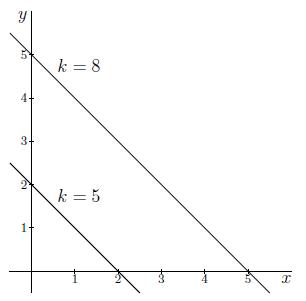
De tweede niveaukromme, met waarde $k=8$, tekenen we op dezelfde manier. We beginnen met het afleiden van de lijn waarop de punten $(x,y)$ liggen die functiewaarde 8 opleveren:
$$\begin{align}
3 + x + y &= 8\\
x + y &= 5\\\
y &= 5- x.
\end{align}$$
We krijgen dus een lineaire functie die de $y$-as snijdt in $(0,5)$ en een richtingscoëfficiënt van $-1$ heeft. Als we deze lijn tekenen, krijgen we onderstaande grafiek. Hierin is ook de niveaukromme met waarde $k=5$ getekend.
