Welke van de onderstaande grafieken geeft de niveaukrommen van $z(x,y)=x^2 + y^2$ met waarden $k=1$ en $k=4$ weer?
Antwoord 1 correct
Correct
Antwoord 2 optie
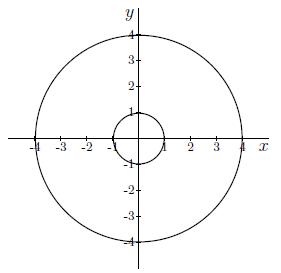
Antwoord 2 correct
Fout
Antwoord 3 optie
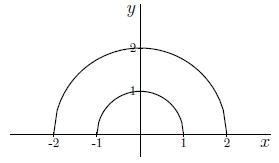
Antwoord 3 correct
Fout
Antwoord 4 optie
Het is niet mogelijk om de niveaukrommen van deze functie te tekenen, want $z(x,y)=k$ kun je niet herschrijven.
Antwoord 4 correct
Fout
Antwoord 1 optie
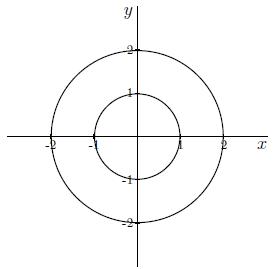
Antwoord 1 feedback
Correct: Het herschrijven van $x^2 + y^2 = k$ voor $k=1$ geeft:
$$ x^2 + y^2 = 1 \iff y^2 = 1-x^2 \iff y = \pm\sqrt{1-x^2}.$$
Als je de grafiek hiervan tekent, krijg je de middelste cirkel; misschien herken je in $x^2+y^2=1$ ook wel de cirkelvergelijking met middelpunt $(0,0)$ en straal $\sqrt{1}=1$. Het herschrijven van $x^2 + y^2 = k$ voor $k=4$ geeft:
$$ x^2 + y^2 = 4 \iff y^2 = 4-x^2 \iff y = \pm\sqrt{4-x^2}.$$
Als je de grafiek hiervan tekent, krijg je de buitenste cirkel; misschien herken je in $x^2+y^2=4$ ook wel de cirkelvergelijking met middelpunt $(0,0)$ en straal $\sqrt{4}=2$.
Ga door.
$$ x^2 + y^2 = 1 \iff y^2 = 1-x^2 \iff y = \pm\sqrt{1-x^2}.$$
Als je de grafiek hiervan tekent, krijg je de middelste cirkel; misschien herken je in $x^2+y^2=1$ ook wel de cirkelvergelijking met middelpunt $(0,0)$ en straal $\sqrt{1}=1$. Het herschrijven van $x^2 + y^2 = k$ voor $k=4$ geeft:
$$ x^2 + y^2 = 4 \iff y^2 = 4-x^2 \iff y = \pm\sqrt{4-x^2}.$$
Als je de grafiek hiervan tekent, krijg je de buitenste cirkel; misschien herken je in $x^2+y^2=4$ ook wel de cirkelvergelijking met middelpunt $(0,0)$ en straal $\sqrt{4}=2$.
Ga door.
Antwoord 2 feedback
Fout: Let op het herschrijven van $z(x,y)=k$. De straal van de buitenste cirkel is niet gelijk aan 4.
Zie Voorbeeld 1 en Voorbeeld 2.
Zie Voorbeeld 1 en Voorbeeld 2.
Antwoord 3 feedback
Fout: Let op het herschrijven van $z(x,y)=k$. Denk eraan dat je bij $y^2 = \ldots$ na het worteltrekken altijd twee oplossingen krijgt.
Zie Voorbeeld 1 en Voorbeeld 2.
Zie Voorbeeld 1 en Voorbeeld 2.
Antwoord 4 feedback