Welke van de onderstaande grafieken geeft de indifferentiekrommen van de nutsfunctie U(x,y)=4x34y14, (x,y>0) met waarden k=2, k=4 en k=8 weer?
Antwoord 1 correct
Correct
Antwoord 2 optie
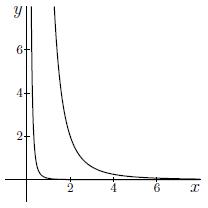
Antwoord 2 correct
Fout
Antwoord 3 optie
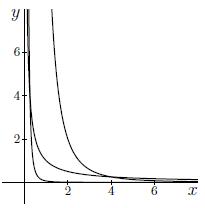
Antwoord 3 correct
Fout
Antwoord 4 optie
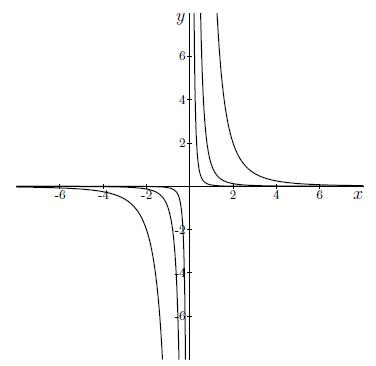
Antwoord 4 correct
Fout
Antwoord 1 optie
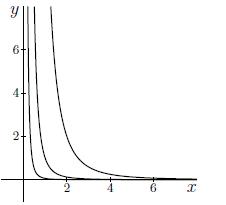
Antwoord 1 feedback
Correct: Het herschrijven van 4x34y14=k voor k=2 geeft:
4x34y14=2⟺y14=12x34⟺y=±116x3y≥0=116x3.
Als je de grafiek hiervan tekent, krijg je de meest linkse kromme. Het herschrijven van 4x34y14=k voor k=4 geeft:
4x34y14=4⟺y14=1x34⟺y=±1x3y≥0=1x3.
Als je de grafiek hiervan tekent, krijg je de middelste kromme. Het herschrijven van 4x34y14=k voor k=8 geeft:
4x34y14=8⟺y14=2x34⟺y=±16x3y≥0=16x3.
Als je de grafiek hiervan tekent, krijg je de meest rechtse kromme.
Ga door.
4x34y14=2⟺y14=12x34⟺y=±116x3y≥0=116x3.
Als je de grafiek hiervan tekent, krijg je de meest linkse kromme. Het herschrijven van 4x34y14=k voor k=4 geeft:
4x34y14=4⟺y14=1x34⟺y=±1x3y≥0=1x3.
Als je de grafiek hiervan tekent, krijg je de middelste kromme. Het herschrijven van 4x34y14=k voor k=8 geeft:
4x34y14=8⟺y14=2x34⟺y=±16x3y≥0=16x3.
Als je de grafiek hiervan tekent, krijg je de meest rechtse kromme.
Ga door.
Antwoord 2 feedback
Fout: Hoeveel indifferentiekrommen worden er gevraagd?
Probeer de opgave nogmaals.
Probeer de opgave nogmaals.
Antwoord 3 feedback
Fout: Niveaukrommen, en dus ook indifferentiekrommen, kunnen elkaar niet snijden. Waarschijnlijk heb je een foutje gemaakt in het herschrijven.
Zie Niveaukrommen, Voorbeeld 1 en Voorbeeld 2.
Zie Niveaukrommen, Voorbeeld 1 en Voorbeeld 2.
Antwoord 4 feedback
Fout: Let op het domein van x en y.
Probeer de opgave nogmaals.
Probeer de opgave nogmaals.

