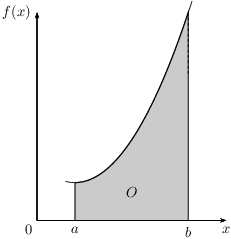
Uit de stelling over integralen en oppervlakte volgt dat er een relatie bestaat tussen een integraal en de oppervlakte onder/boven een grafiek van een functie. Deze relatie zullen we hier verder toelichten. Beschouw daartoe de oppervlakte $O(f,a,b)$ van het gebied ingesloten door de grafiek van een functie $f(x)$, de $x$-as en de lijnen $x=a$ en $x=b$, die in onderstaande figuur is weergegeven.
In het algemeen is het niet eenvoudig om de oppervlakte te berekenen wanneer $f(x)$ geen lineaire functie is. We kunnen wel een schatting geven voor de oppervlakte door het interval $[a,b]$ op te delen in kleinere deelintervallen. Voor ieder van deze deelintervallen bepalen we dan de oppervlakte van het staafje dat het beste past onder de grafiek van $f(x)$. Tellen we de oppervlakten van al deze staafjes op dan geeft dit een goede ondergrens voor de oppervlakte $O(f,a,b)$. In onderstaande figuur gebruiken we bijvoorbeeld drie staafjes om een schatting te maken voor de oppervlakte $O(f,a,b)$, ofwel $O(f,a,b)\approx O_1+O_2+O_3$.
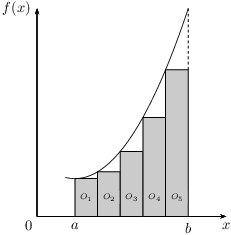
Hoe meer deelintervallen we kiezen, hoe beter de schatting voor de oppervlakte wordt. In onderstaande figuur gebruiken we bijvoorbeeld vijf staafjes om een schatting te maken voor de oppervlakte $O(f,a,b)$, ofwel $O(f,a,b)\approx O_1+O_2+O_3+O_4+O_5$.
Als we het aantal staafjes maar groot genoeg maken zullen we uiteindelijk zo'n goede benadering van de oppervlakte krijgen, dat we het $\approx$-teken mogen vervangen door het $=$-teken, dus $O(f,a,b)=O_1+O_2+\ldots+O_n$, waarbij $n$ een groot getal is.
In het algemeen is het niet eenvoudig om de oppervlakte te berekenen wanneer $f(x)$ geen lineaire functie is. We kunnen wel een schatting geven voor de oppervlakte door het interval $[a,b]$ op te delen in kleinere deelintervallen. Voor ieder van deze deelintervallen bepalen we dan de oppervlakte van het staafje dat het beste past onder de grafiek van $f(x)$. Tellen we de oppervlakten van al deze staafjes op dan geeft dit een goede ondergrens voor de oppervlakte $O(f,a,b)$. In onderstaande figuur gebruiken we bijvoorbeeld drie staafjes om een schatting te maken voor de oppervlakte $O(f,a,b)$, ofwel $O(f,a,b)\approx O_1+O_2+O_3$.
Hoe meer deelintervallen we kiezen, hoe beter de schatting voor de oppervlakte wordt. In onderstaande figuur gebruiken we bijvoorbeeld vijf staafjes om een schatting te maken voor de oppervlakte $O(f,a,b)$, ofwel $O(f,a,b)\approx O_1+O_2+O_3+O_4+O_5$.
Als we het aantal staafjes maar groot genoeg maken zullen we uiteindelijk zo'n goede benadering van de oppervlakte krijgen, dat we het $\approx$-teken mogen vervangen door het $=$-teken, dus $O(f,a,b)=O_1+O_2+\ldots+O_n$, waarbij $n$ een groot getal is.