Oppervlakte

Definitie: Beschouw de functie $f(x)$ op het interval $[a,b]$.

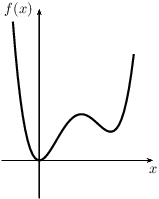
• De functie $f(x)$ is niet-negatief op het interval $[a,b]$ als $f(x)\geq 0$ voor iedere $x\in[a,b]$;
• De functie $f(x)$ is niet-positief op het interval $[a,b]$ als $f(x)\leq 0$ voor iedere $x\in[a,b]$.

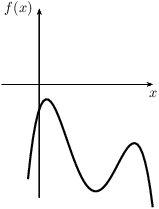niet-negatieve functie	niet-positieve functie

We kunnen het integraalbegrip nu koppelen aan de oppervlakte van een gebied onder de grafiek van een functie.

Stelling:

• Als $f(x)$ een niet-negatieve functie is, dan is de oppervlakte van het gebied ingesloten door de grafiek van $f(x)$, de $x$-as en de lijnen $x=a$ en $x=b$ gelijk aan de integraal $\int_a^b f(x)dx$;
• Als $f(x)$ een niet-positieve functie is, dan is de oppervlakte van het gebied ingesloten door de grafiek van $f(x)$, de $x$-as en de lijnen $x=a$ en $x=b$ gelijk aan de integraal $-\int_a^b f(x)dx$.

Opmerking: Voor een functie die deels niet-negatief is en deels niet-positief, dienen we het integratieinterval $[a,b]$ op te splitsen in deelintervallen, zodanig dat de functie op ieder deelinterval niet-negatief of niet-positief is.